Định nghĩa và công thức của số hữu tỉ là một trong những kiến thức vô cùng quan trọng mà học sinh THPT cần nắm được. Để xây dựng một nền tảng toán học vững chắc, chúng ta hãy cùng điểm qua tất cả các yếu tố để tìm hiểu về số hữu tỉ trong bài viết này nhé!
Số hữu tỉ là gì?
Trong toán học, cụ thể là đại số, số hữu tỉ là số x có thể biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên với b khác 0 . Tập hợp các số hữu tỉ hay còn gọi là trường số hữu tỉ được kí hiệu là Q.
Số hữu tỉ là số viết được dưới dạng a/b với a, b Z, b ≠ 0 và kí hiệu là Q
Ví dụ: Các số 3; -1/2; 2/3;… là các số hữu tỉ
Bộ số hữu tỉ bao gồm:
-
Số thập phân hữu hạn: 0,5 (½), 0,2 (⅕),…
-
Số thập phân tuần hoàn vô hạn: 0,16666… (⅙), 0,3333… (⅓),…
-
Tập hợp các số nguyên (Z): -2, -1, 0, 1, 2,…
-
Tập hợp các số tự nhiên (N): 1, 2, 3, 4, 5, 6,…
Tính chất của số hữu tỉ:
-
Tập hợp các số hữu tỉ là tập hợp đếm được.
-
Phép nhân các số hữu tỉ có dạng
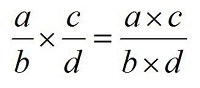
-
Phép chia số hữu tỉ có dạng:
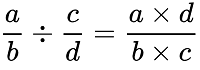
-
Nếu hữu tỉ là hữu tỉ dương thì hữu tỉ ngược lại là hữu tỉ âm và ngược lại. Tức là tổng của số hữu tỉ và số đối của nó bằng 0.
Số vô tỷ là gì?
Trong toán học, số vô tỷ là tất cả các số thực không phải là số hữu tỉ, mà là các số được tạo thành từ các tỷ số (hoặc phân số) của các số nguyên.
Số vô tỷ là gì? Số vô tỉ là số viết được dưới dạng số thập phân vô hạn tuần hoàn. Và kí hiệu của số vô tỉ là I.
Bạn cần lưu ý rằng số thực không phải là số hữu tỉ , nghĩa là bạn không thể biểu diễn chúng dưới dạng tỷ lệ như a/b (trong đó a, b là số nguyên).
Tính chất của số vô tỉ: Tập hợp các số vô tỉ là tập hợp không đếm được.
Ví dụ:
-
Số vô tỷ: 0.1010010001000010000010000001… (đây là số thập phân vô hạn tuần hoàn)
-
Số căn bậc hai 2: 2 (căn 2)
-
Số pi (π): 3.14159 26535 89793 23846 26433 83279 50 288…..
Sự khác biệt giữa hữu tỉ và số vô tỷ
-
Các số hữu tỉ bao gồm các số thập phân tuần hoàn vô hạn và các số vô tỉ là các số thập phân vô hạn không lặp lại.
-
hữu tỉ chỉ là phân số, còn số vô tỷ có rất nhiều loại số khác nhau
-
hữu tỉ là số đếm được, số vô tỉ là không đếm được
Các loại số hữu tỉ thông dụng
hữu tỉ gồm những số nào? Thì trong toán học sẽ có 2 loại số hữu tỉ là số hữu tỉ âm và số hữu tỉ dương. Đặc biệt:
- hữu tỉ âm: Bao gồm tất cả các số hữu tỉ nhỏ hơn 0
- hữu tỉ dương: Bao gồm tất cả sách hữu tỉ lớn hơn 0
- Lưu ý: số 0 không phải là số hữu tỉ âm cũng không phải là số hữu tỉ dương.

Các phép toán cơ bản với số hữu tỉ
Trong chương trình toán từ lớp 7 trở lên, các em sẽ được làm quen với các phép toán cơ bản với số hữu tỉ như sau:
1. Phép cộng và phép trừ
Sau đây là các bước mà bạn có thể áp dụng để tính các phép tính cộng trừ với số hữu tỉ.
Bước 1: Viết các số hữu tỉ dưới dạng phân số
Bước 2: Vận dụng quy tắc cộng, trừ và các tính chất để tính
Quy tắc cộng, trừ: Đưa các số hữu tỉ về cùng mẫu số (đồng quy, bớt,…) rồi cộng, trừ tử số, giữ nguyên mẫu số.
Tự nhiên:
-
Tính chất giao hoán: x + y = y + x
-
Thuộc tính kết hợp: (x + y) + z = x + (y + z)
-
Tính chất cộng 0: x + 0 = 0 + x = x
Bước 3: Đơn giản hóa kết quả (nếu có thể)
2. Phép nhân và phép chia
-
Nhân hai số hữu tỉ:
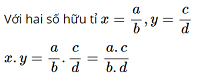
-
Chia hai số hữu tỉ:
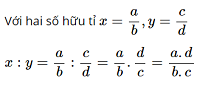
3. Các phép tính và công thức toán khác hữu tỉ
Ngoài các phép tính cơ bản trên, bạn cũng cần lưu ý một số phép tính và công thức phổ biến liên quan đến hữu tỉ sau đây.
Giá trị tuyệt đối của một số hữu tỉ
Giá trị tuyệt đối của một số hữu tỉ x, ký hiệu là |x|, là khoảng cách từ điểm x đến điểm O trên trục số.
-
Nếu x > 0 thì |x| = x.
-
Nếu x = 0 thì |x| = 0.
-
Nếu x < 0 thì |x| = -x.
Dựa vào định nghĩa trên, công thức xác định giá trị tuyệt đối của một số hữu tỉ như sau:
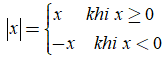
Công thức tính lũy thừa của một số hữu tỉ:
Các công thức tính lũy thừa của một số hữu tỉ mà các em cần lưu ý:

Cách so sánh hai số hữu tỉ
Để so sánh hai số hữu tỉ x, y ta có thể làm như sau:
-
Viết x và y dưới dạng phân số có mẫu số dương.
x = a /m; y = b/m ( m > 0)
-
So sánh các số nguyên a và b
-
Nếu a > b thì x > y
-
Nếu a = b thì x = y
-
Nếu a < b thì x < y
-
Các dạng bài tập dãy số hữu tỉ thường gặp và cách giải
Dưới đây là một số dạng bài tập hữu tỉ thường gặp và cách giải để các bạn tham khảo và vận dụng:
Dạng 1: Thực hiện phép tính
Phương pháp giải: Đầu tiên, các em cần viết hai số hữu tỉ đã cho dưới dạng phân số, sau đó tiến hành áp dụng các quy tắc tính để tính và đưa ra đáp số đúng, cũng như rút gọn kết quả nếu có thể.
Lưu ý: Chỉ áp dụng thuộc tính:
- ab + ac = a.(b+c)
- ac + bc = (a+b).c)
Không áp dụng: a:b + a:c = a:(b+c)
Ví dụ:

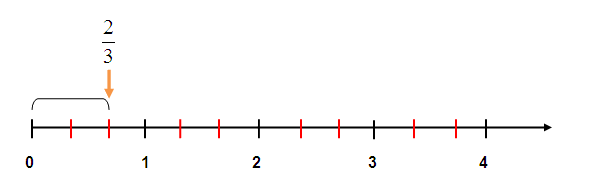
Dạng 2: Biểu diễn số hữu tỉ trên trục số
Phương pháp giải:
- Trường hợp a/b là số dương hữu tỉ: ta chia khoảng có độ dài 1 đơn vị thành b phần bằng nhau. Sau đó tiến hành lấy theo chiều dương của trục Ox một phần. Bây giờ chúng ta sẽ lấy vị trí của số a/b.
- Trường hợp a/b là số âm hữu tỉ: ta chia khoảng có độ dài 1 đơn vị thành b phần bằng nhau. Sau đó tiến hành lấy theo chiều âm của trục Ox một phần. Bây giờ chúng ta sẽ lấy vị trí của số a/b.
Ví dụ: Biểu diễn số 5/4
Dung dịch:
Ta thấy rằng 5/4 là một số hữu tỉ dương. Bây giờ ta chia khoảng ứng với độ dài 1 đơn vị thành 4 phần bằng nhau. Lấy 5 phần ta sẽ biểu diễn phân số 5/4.
Dạng 3: So sánh các số hữu tỉ
Phương pháp giải: Ta sẽ cho các số hữu tỉ đã cho dưới dạng phân số có cùng mẫu số dương rồi so sánh các tử số. Ngoài ra, bạn cũng có thể so sánh với 0, so sánh với 1, -1 hay dựa vào phần bù 1 cũng như so sánh với các phân số trung gian để tìm ra đáp án đúng.
Ví dụ: So sánh các số hữu tỉ sau:
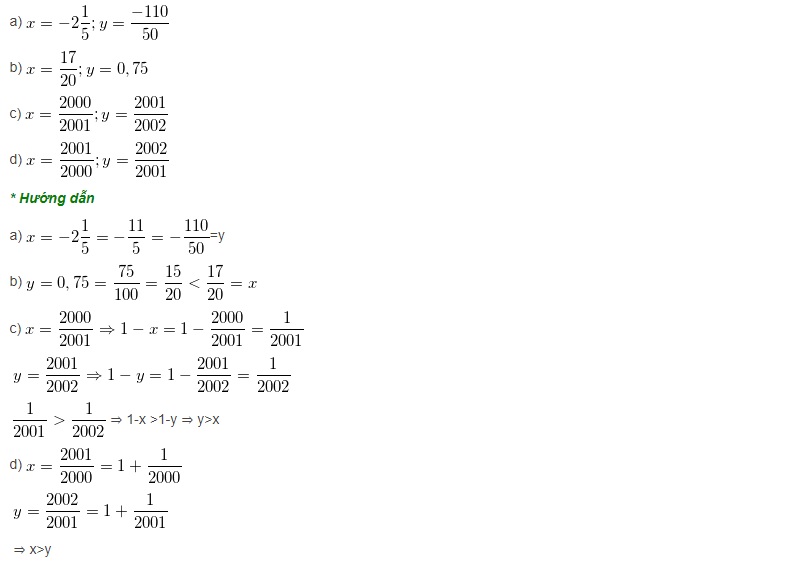
Dạng 4: Tìm điều kiện để một số hữu tỉ âm, dương hoặc 0
Phương pháp giải: Học sinh dựa vào tính chất của số hữu tỉ để xác định số đó âm, dương hay bằng 0.
Ví dụ:

Dạng 5: tìm số hữu tỉ trong dãy số
Phương pháp giải: Đưa các số hữu tỉ đó về cùng mẫu số hoặc tử số.

Dạng 6: Tìm x để biểu thức nguyên
Phương pháp giải: Trường hợp tử số không chứa x ta dùng dấu hiệu chia hết, nếu tử số chứa x ta dùng dấu hiệu chia hết hoặc áp dụng phép tách tử số cho mẫu số. Đối với các bài toán tìm đồng thời cả x và y, ta sẽ nhóm x hoặc y rồi rút gọn thành phân số.

Dạng 7: Các bài toán tìm x với dãy số hữu tỉ
Phương pháp giải: Trước hết ta phải rút gọn mẫu số, sau đó chuyển các số hạng chứa x sang một vế, các số hạng còn lại sang một vế (đổi dấu) rồi tiến hành tìm x.
Ví dụ:

Dạng 8: Bài toán tìm x trong bất phương trình
Phương pháp giải:

Ví dụ: Tìm x, biết:
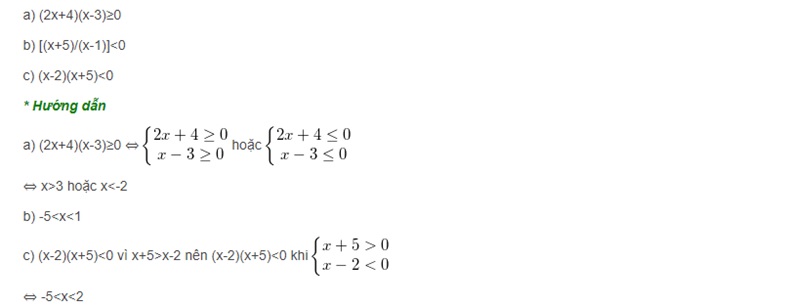
Dạng 9: Các bài toán tính tổng hữu tỉ theo quy tắc
* Quy tắc 1: Tính tổng của dãy số có các số hạng cách nhau bởi một số không đổi
Phương pháp giải:

* Quy tắc 2: Tính tổng của dãy số có các số hạng mà số liền sau gấp n lần số liền trước.
Phương pháp giải: Tiến hành phân tích từ số đến hiệu của 2 số (số cuối – số đầu) cùng vế mẫu số.
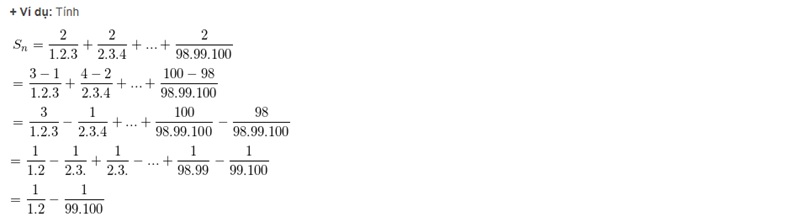
Một số bài tập mẫu về dãy số hữu tỉ tự luyện

Hi vọng qua những chia sẻ trên của manta.edu.vn đã giúp các bạn phần nào hiểu được khái niệm và các công thức tính về số hữu tỉ. Đồng thời, qua đó hỗ trợ các bạn xây dựng và tiếp thu kiến thức nâng cao trên lớp tốt hơn. Xin được ở bên bạn.



