Hàm số đồng biến khi nào? Đây có lẽ là câu hỏi khiến nhiều bạn học sinh bối rối. Đừng lo! Trong bài viết này, Manta.edu.vn sẽ giúp các bạn hệ thống hóa toàn bộ kiến thức một cách toàn diện nhất. Cùng theo dõi và đừng bỏ lỡ những thông tin dưới đây nhé!
Tổng quan lý thuyết về Hàm số đồng biến
Khi học trong trường trước khi đi vào một vấn đề mới. Chúng em thường được thầy dạy cho quen dần các khái niệm, định nghĩa. Khi hiểu được lý thuyết, chúng ta có thể áp dụng nó để giải quyết vấn đề. Vậy trước tiên để học tốt về Hàm số đồng biến bạn cần hiểu hàm là gì?
Hàm số là gì?
Một cách trực quan nhất, hàm số được coi là một quá trình liên kết các phân tử của chính tập hợp X với một phần tử nào đó trong tập hợp Y.
Về mặt hình thức, đối với một hàm f được xác định từ tập X đến tập Y bởi tập G. Bao gồm các cặp có thứ tự (x, y) và x thuộc X, y thuộc Y. Có thể hiểu theo nghĩa một cách khác, với mọi x trong X sẽ có đúng một phần tử của y. Và các cặp có thứ tự (x, y) đều phải thuộc tập hợp các cặp xác định hàm f.
Giả sử tập G được gọi là đồ thị của hàm số. Về mặt hình thức, tập G có thể được xác định bởi hàm trên. Đồng thời hàm số thường được phân biệt với chính đồ thị của nó.
Hàm còn được gọi là ánh xạ, mặc dù có một số lý thuyết phân biệt giữa hàm và ánh xạ. Đối với định nghĩa của hàm, X và Y sẽ được gọi là tập hợp và miền xác định. Nếu (x, y) cùng thuộc một tập f thì y là ảnh của x qua f. Hoặc ngược lại giá trị của f cũng sẽ được áp dụng cho đối số của x.
Cụ thể hơn, với ngữ cảnh của các con số, y sẽ là giá trị của f cho giá trị của x. Hay ngắn gọn hơn, y sẽ là giá trị của f của x và được ký hiệu là y = f(x).
Nếu miền xác định và tập xác định của f và g là như nhau thì ta nói hai hàm số f và g bằng nhau. Cụ thể là f = g nếu f(x) = g(x) trong đó x thuộc X, trong đó f: X → Y và g: X → Y.
Hàm số đồng biến là gì?
Hàm số đồng biến là một trong những kiến thức trọng tâm của môn Toán. Đầu tiên để biết khi Hàm số đồng biến. Bạn cần hiểu Hàm số đồng biến là gì?
Gọi K là một khoảng, nửa hoặc đoạn và hàm số y = f(x) là hàm số xác định trên K. Ta có hàm số y = f(x) gọi là đồng biến hoặc tăng trên K, nếu: Với mọi x1, x2 thuộc K nhưng x1 < x2 thì f(x1) < f(x2)
Biểu diễn đồ thị của hàm này là một đường hướng lên. Khi hàm số nghịch biến hoặc đồng biến trên K, nó còn được gọi là hàm số đơn điệu trên K.
Hàm số đồng biến khi nào?
Cho hàm số f được gọi là đồng biến trên K khi:
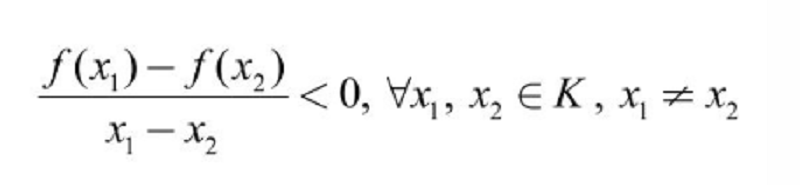
Cho hàm số f xác định có đạo hàm trên K. Nếu f'(x) > 0 với mọi x thuộc K thì hàm số sẽ đồng biến trên K. Qua đó bạn có thể biết Hàm số đồng biến khi nào và cần điều kiện gì. Đồng thời, nó cũng là điều kiện cần và đủ để hàm số đơn điệu.
Để bạn đọc hiểu rõ hơn vấn đề này, chúng ta cùng đi vào ví dụ điển hình sau: Xét tính nghịch biến và đồng biến của hàm số, dựa vào bảng tìm Hàm số đồng biến trên khoảng nào?
![]()
Hướng dẫn giải:
Ta có tập xác định D = R và y’= 3 – 2x; Cho y’ = 0 3 – 2x = 0 x = 3/2
Vậy khi x = 3/2 thì y = 25/4
Ta có bảng biến thiên sau:
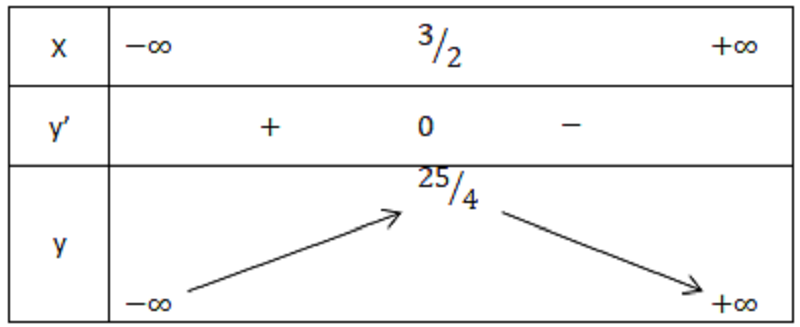
Thông qua bảng trên, bạn có thể xác định Hàm số đồng biến trên phạm vi từ âm vô cực đến 25/4.
Các dạng bài toán thường gặp về khoảng Hàm số đồng biến
Để hiểu rõ hơn về kiến thức Hàm số đồng biến. Sau đây chúng ta sẽ cùng nhau tìm hiểu 5 dạng bài tập về khoảng Hàm số đồng biến.
Dạng 1: Tìm m để Hàm số đồng biến trên R, nghịch biến trên R
Với dạng toán này các bạn sẽ làm quen với đa thức bậc 3. Ta sẽ có công thức sau:

Bài tập ứng dụng:

Dạng 2: Tìm m để Hàm số đồng biến nghịch biến trên từng khoảng xác định
Với dạng toán tìm m Hàm số đồng biến trên một khoảng ta sẽ thường gặp ở hàm phân thức tuyến tính hay còn gọi là hàm phân thức bậc nhất. Áp dụng công thức sau để giải các bài toán về Hàm số đồng biến trên từng khoảng xác định hoặc nghịch đảo.

Bài tập ứng dụng:

Dạng 3: Nhẩm tìm nghiệm của đạo hàm
Bài tập ứng dụng: Cho hàm số y = x³ – (m+1)x² – (m²-2m)x + 2020. Tìm m để hàm số nghịch biến trên khoảng (0;1).
Hướng dẫn giải:

Dạng 4: Cô lập tham số m
Bài tập ứng dụng:
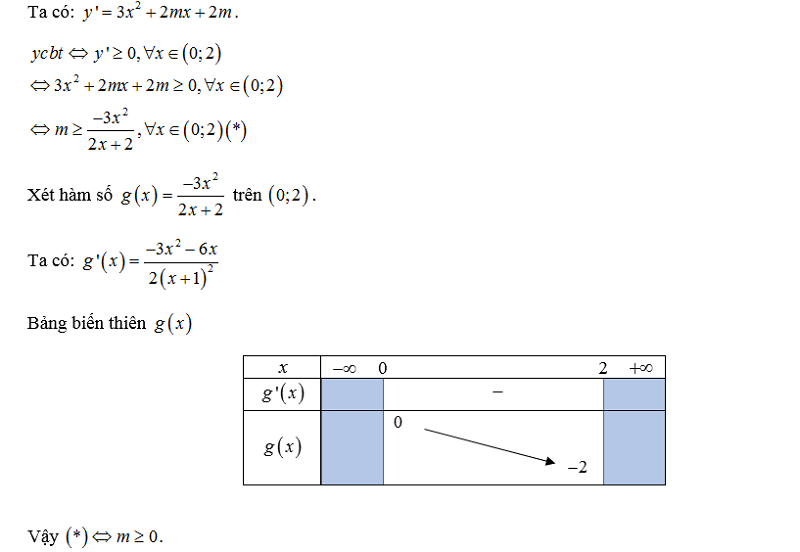
Cho hàm số y = x³ + mx² + 2mx + 3. Tìm điều kiện của m để hàm số luôn đồng biến trên khoảng (0,2).
Hướng dẫn giải:
Dạng 5: Hàm số tuyến tính đơn điệu trên một khoảng cho trước
Nếu hàm tuyến tính có tham số thì hàm suy biến dễ xảy ra. Ta cần xét trường hợp hàm suy biến trở thành hàm bậc nhất. Công thức xác định để xét một hàm suy biến như sau:

Bài tập ứng dụng:
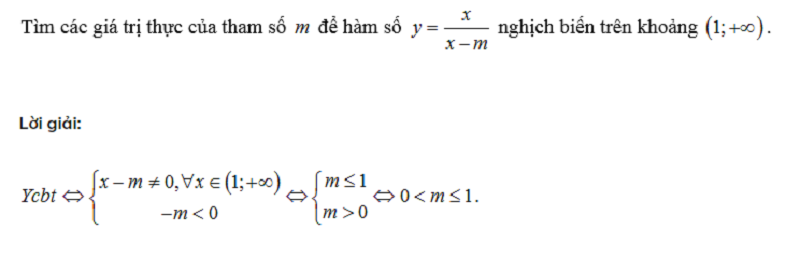
Xem thêm: Đạo hàm là gì? Các khái niệm và công thức đạo hàm từ cơ bản đến nâng cao
Một số mẹo tính nhanh bài tập toán Hàm số đồng biến
Khi giải bài tập Toán đặc biệt với các dạng trắc nghiệm. Chúng ta không chỉ cần biết các công thức và lý thuyết. Nhưng cũng cần một mẹo nhỏ để tính nhanh đáp số. Sau đây là một số mẹo giúp bạn giải nhanh bài tập trắc nghiệm Hàm số đồng biến.
Ví dụ: Tìm Hàm số đồng biến trên khoảng R
A. y = (x2+1)2–3x
B. y = x – 1/x
C. y = x–1x
Hướng dẫn giải:
Mẹo 1: Làm từ trái sang phải
Chọn đáp án B. Ta có với A thì y'(0) = -3 < 0 nên đáp án A bị loại. Với ý B, y’ > 0 với mọi x thuộc R. Vậy đáp án B đúng nên ta dừng tại đây.
Mẹo 2: Sử dụng bài kiểm tra
-
Đầu tiên, Hàm số đồng biến trên R chắc chắn sẽ phải xác định trên R. Do đó, đáp án C và D sẽ bị loại.
-
Với đáp án A vì A là hàm bậc hai nên sẽ có đạo hàm cấp 3. Hơn nữa đa thức bậc 3 sẽ không dương nên ta tiếp tục loại đáp án A. Do đó chỉ có đáp án B là đúng nhất.
-
Lời bình: Vậy để tìm ra đáp án nhanh nhất cho bài toán trên. Bạn có thể sử dụng một trong hai mẹo mà Manta.edu.vn gợi ý ở trên. Dù bằng cách nào thì bạn vẫn phải tính đạo hàm của hàm số đó để có đáp án nhanh nhất.
Trên đây là những kiến thức về Hàm số đồng biến mà Manta.edu.vn muốn gửi đến toàn thể bạn đọc. Với mong muốn lan tỏa tri thức đến các bạn trẻ trên khắp mọi miền đất nước. Manta.edu.vn chúc các bạn học tốt môn Toán!



