Công thức đạo hàm nguyên hàm mà các chuyên đề có công thức giải đạo hàm thường gặp trong các bài tập, đề thi toán. Để giúp các em học tập, ghi nhớ và luyện tập hiệu quả, hãy cùng Manta.edu.vn tìm hiểu rõ hơn ngay trong bài viết sau.
Đạo hàm nguyên hàm là gì?
Trong chương trình đại số THPT nói chung và lớp 11 nói riêng, các em học sinh sẽ làm quen với chủ đề đạo hàm và nguyên hàm . Đây được coi là kiến thức quan trọng , bởi nó sẽ xuất hiện phổ biến trong các kỳ thi không chỉ lớp 11 mà cả lớp 12, tốt nghiệp, đại học trở lên vẫn phải học.

Do đó, nắm vững lý thuyết là bước đầu tiên cần ghi nhớ. Đặc biệt:
Đạo hàm của hàm số được hiểu là sự mô tả sự biến thiên của hàm số tại một điểm nào đó.
Và nguyên hàm của một hàm thực f đã cho là một hàm F sẽ có đạo hàm bằng f. Bây giờ F’ = f. Do đó, quá trình tìm nguyên hàm được gọi là tích phân bất định. Trên thực tế, việc xác định một biểu thức cho nguyên hàm còn khó hơn là tìm đạo hàm.
Bảng Công thức đạo hàm nguyên hàm chi tiết
Để có thể giải được các bài toán về đạo hàm và nguyên hàm, ngoài việc nắm vững lý thuyết, học sinh còn cần thuộc lòng các công thức của từng dạng.
Dưới đây là công thức chi tiết của 2 dạng toán này để các bạn tham khảo:
công thức đạo hàm
Việc ghi nhớ các công thức đạo hàm cơ bản và nâng cao sẽ giúp các em giải các bài toán chính xác hơn. Đặc biệt:
Công thức phái sinh cơ bản

Hai hàm phân số hữu tỉ có đạo hàm:
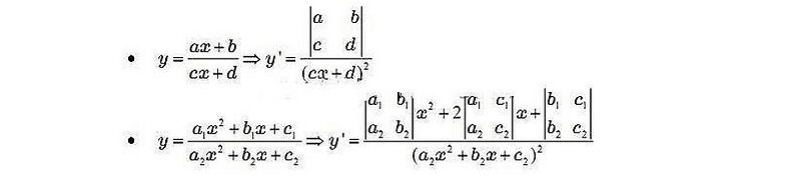
Quy tắc đạo hàm của hàm hợp: Nếu y = y(u(x)) thì y'(x) = y'(u) . u'(x).
Đạo hàm của hàm sơ cấp

Bảng đạo hàm cấp cao:
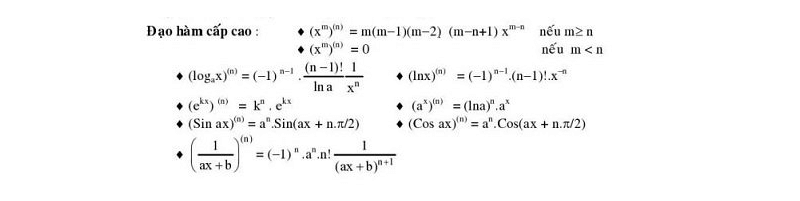
Công thức nguyên hàm
Thuộc tính của nguyên hàm:
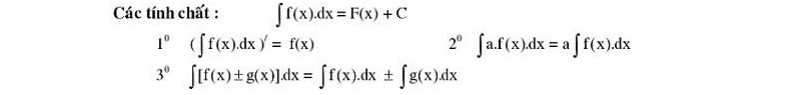
Bảng nguyên hàm cơ bản
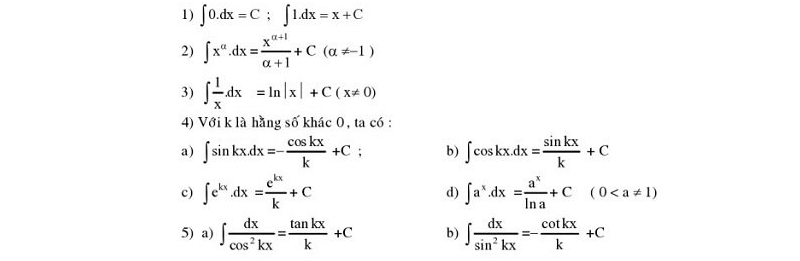
Bảng nguyên hàm mở rộng

Các dạng bài tập áp dụng đạo hàm, công thức nguyên hàm thường gặp
Đối với việc giải đạo hàm và nguyên hàm, sau khi nắm vững lý thuyết về định nghĩa và công thức thì việc biết các dạng toán của nó cũng rất quan trọng.
Vì chỉ khi biết bài toán thuộc dạng gì thì việc áp dụng đúng công thức để giải chính xác bài toán sẽ dễ dàng hơn. Vì vậy, đây là một số dạng bài tập mà bạn có thể sẽ gặp phải liên quan đến nguyên hàm và đạo hàm:
Các dạng toán về đạo hàm
Dạng 1: Tính đạo hàm của hàm số
Phương pháp giải: Ở dạng toán đạo hàm này các em sẽ phải vận dụng các quy tắc và cách tính đạo hàm, đặc biệt là công thức tính đạo hàm hợp số.
Còn trường hợp đề bài yêu cầu tính đạo hàm tại 1 điểm thì mọi người sẽ phải tính đạo hàm trước, sau đó thay vào mới ra kết quả chính xác.
Ví dụ:
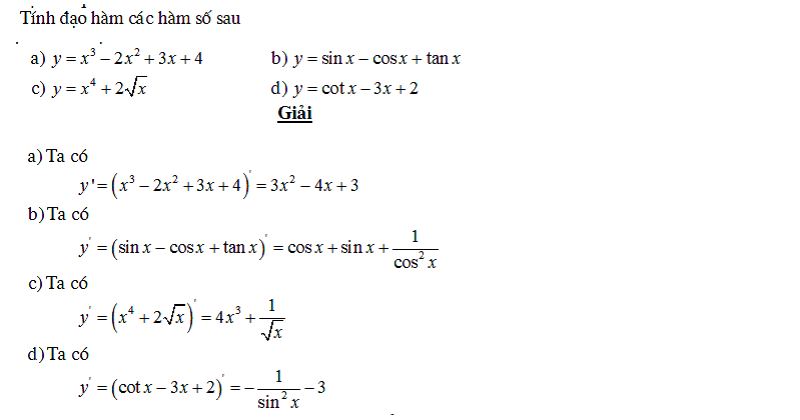
Dạng 2: Giải phương trình y’ = 0
Phương pháp giải: Dạng toán này yêu cầu các em tính y’ trước rồi mới tiến hành giải phương trình y’ = 0.
Ví dụ:

Dạng 3: Chứng minh đẳng thức của đạo hàm
Phương pháp giải: Dạng bài tập này sẽ yêu cầu học sinh tính đạo hàm, đồng thời sẽ vận dụng công thức các phép biến đổi đặc biệt liên quan đến hàm số lượng giác để tính toán.
Ví dụ: Chứng minh rằng:
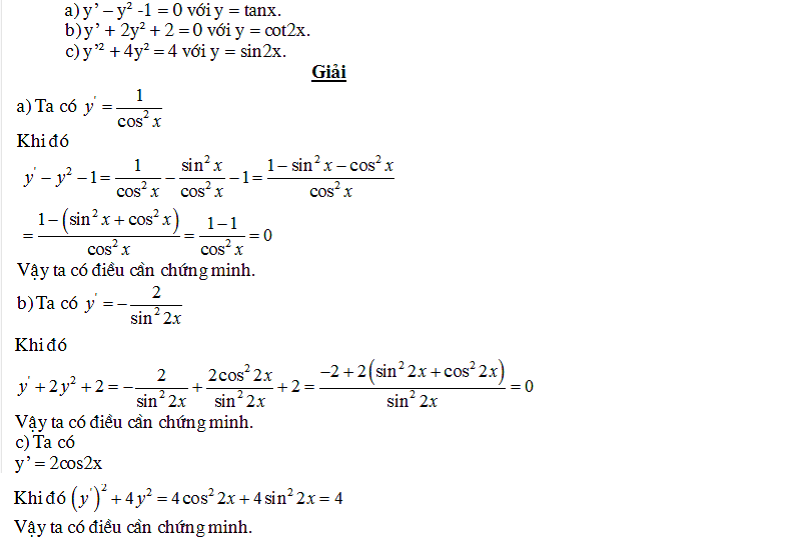
Các dạng toán về nguyên hàm
Trong bài tập về nguyên hàm sẽ có các dạng toán cơ bản như sau:
Dạng 1: Nguyên hàm từng phần

Dạng 2: Nguyên hàm của hàm số lượng giác
Phương pháp giải: Yêu cầu học sinh nắm chắc công thức tính nguyên hàm với các hàm lượng giác sơ cấp và các hàm lượng giác cơ bản.
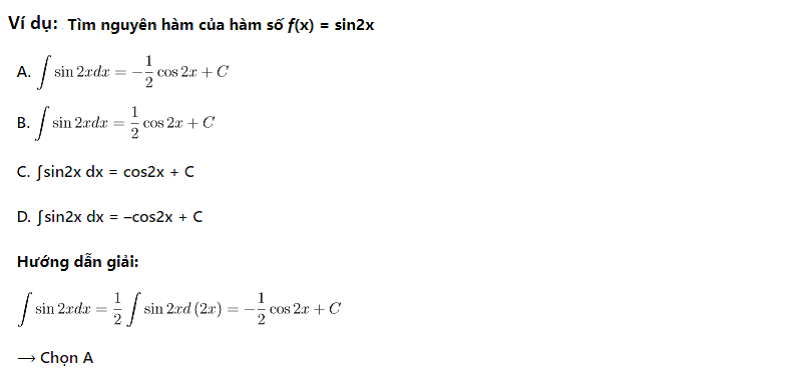
Dạng 3: Nguyên hàm của hàm số mũ, logarit
Phương pháp giải: Học sinh cần ghi nhớ cũng như vận dụng đúng công thức nguyên hàm của hàm số mũ, logarit để giúp tính toán chính xác và nhanh chóng hơn.
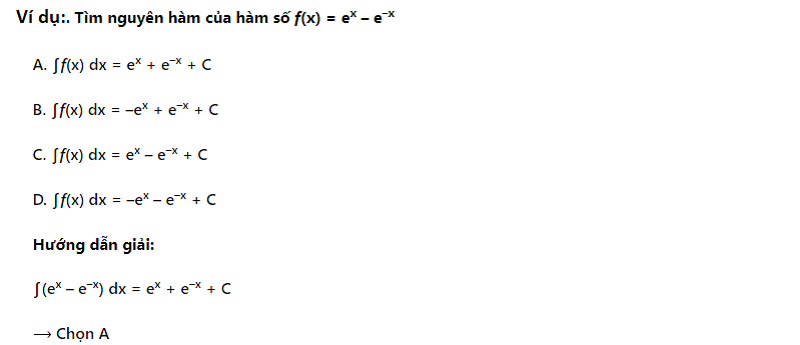
Dạng 4: Nguyên hàm của hàm chứa nghiệm
Phương pháp giải: Áp dụng công thức tính nguyên hàm chứa hàm căn tương ứng
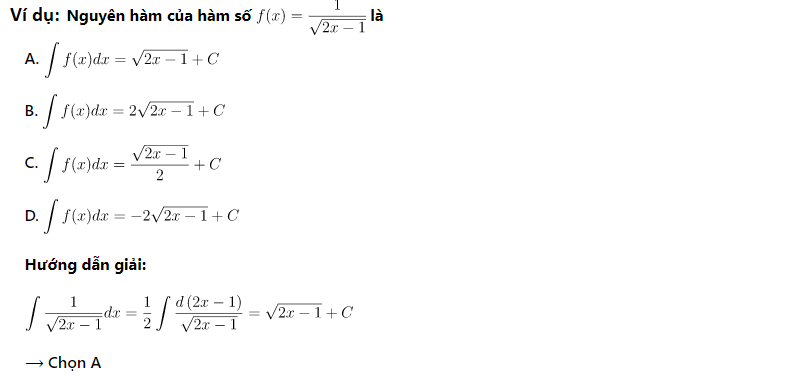
Một số bài tập Công thức đạo hàm nguyên hàm tự luyện
Để giúp các em ghi nhớ các kiến thức trên, sau đây là một số bài tập mẫu từ cơ bản đến nâng cao của cả đạo hàm và nguyên hàm mà các em bắt đầu tự luyện tập:
bài tập đạo hàm

Bài tập về nguyên hàm

Mẹo nhớ công thức đạo hàm, nguyên hàm và áp dụng hiệu quả
Để có thể ghi nhớ công thức tính đạo hàm cũng như nguyên hàm, các bạn có thể áp dụng một số mẹo cơ bản như sau:

- Luyện tập thường xuyên: Làm bài tập và áp dụng công thức thường xuyên sẽ hình thành thói quen sử dụng công thức và áp dụng chính xác hơn.
- Nắm chắc phương pháp giải toán: Như đã giải thích ở trên, mỗi dạng toán có một phương pháp giải riêng nên khi biết dạng các em chỉ cần áp dụng công thức là được.
- Chinh phục nhiều dạng toán và nhiều dạng bài toán: Ngoài việc làm bài tập trên sách giáo khoa sạch đẹp, các em nên tìm kiếm nhiều bài tập trên sách tham khảo, sách luyện thi toán lớp 11, 12, trên mạng, đề thi các năm trước,…
- Áp dụng công thức tính đạo hàm nhanh, nguyên hàm nhanh: Mỗi bài toán đều có công thức tính nhanh nên trong quá trình học và thực hành, học sinh sẽ rút ra kinh nghiệm tính nhanh cho riêng mình.
Phần kết luận
Trên đây là thông tin về kiến thức Công thức đạo hàm nguyên hàm . Qua đó có thể thấy đây là hai chuyên đề quan trọng trong chương trình đại số THPT. Vì vậy, đòi hỏi các em phải nắm chắc kiến thức để chinh phục các kỳ thi với kết quả tốt nhất.



