Đạo hàm lượng giác là các hàm tuyến tính được sử dụng rộng rãi trong hình học và vật lý. Tuy nhiên, các hàm này khá khó nhớ, đặc biệt là hàm Đạo hàm Arctan X gây khó khăn cho người học. Vì vậy để có thể hiểu và nhớ lâu hơn chúng ta cần hiểu bản chất của nó cũng như thường xuyên luyện tập. Hãy cùng tìm hiểu về đạo hàm của arctan x qua bài viết dưới đây nhé!

Hàm y = arctan x là gì?
Để tìm hiểu về Đạo hàm Arctan X, trước tiên chúng ta cần hiểu công thức nguyên hàm của nó là y = arctan x. Vậy hàm y = arctan x là gì? Hãy cùng tìm hiểu định nghĩa, dạng đồ thị và các quy tắc cần nhớ về hàm số này ngay sau đây nhé!
Định nghĩa
Theo định nghĩa, hàm y = arctan x là một tiếp tuyến nghịch đảo của x khi x thuộc tập hợp các số thực ( x=R). Nếu hàm tiếp tuyến của y bằng x với công thức tan y = x, thì arctan của x sẽ bằng hàm tiếp tuyến nghịch đảo của x với công thức y = arctan x = tan ^(-1) . x
Ví dụ: Cho y = arctan x trong đó x bằng 1. Vậy y = arctan 1 = tan ^(-1). 1 = / 4 rad = 45°
hình dạng đồ thị
Đồ thị của hàm số y = arctan x hay còn gọi là f(x) = arctan x có dạng một đường cong tiếp tuyến đối xứng qua trục tọa độ. Hàm số nằm trong góc phần tư thứ nhất và thứ ba, cách đều trục tung.
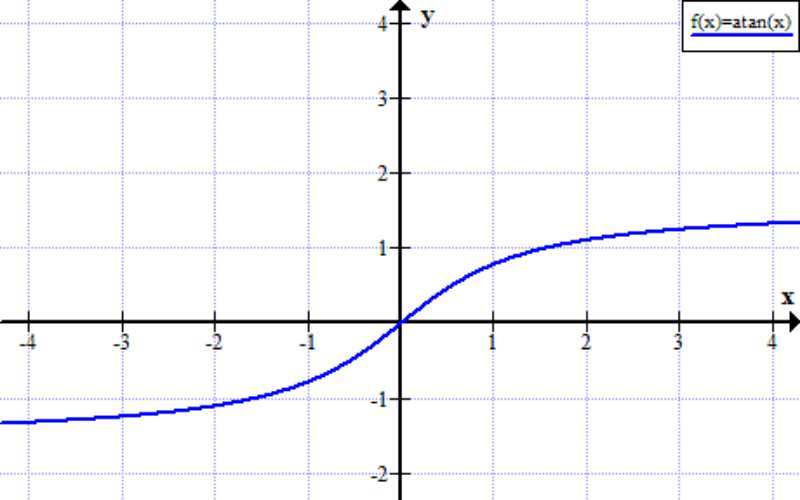
Quy tắc cần nhớ
Để áp dụng được hàm số y = arctan x trong giải toán ta cần nắm được các quy tắc của hàm số arctan để có thể vận dụng một cách linh hoạt. Bảng dưới đây chúng tôi đã hệ thống hóa các quy tắc cần nhớ của hàm này.
Quy tắc Arctan
|
Quy tắc |
quy ước |
|
Tan của arctan x |
tan ( arctan x ) = x |
|
Arctan của đối số phủ định với arctan x |
arctan ( – x ) = – arctan x |
|
Arctan của tổng số |
arctan α + arctan β = arctan [ ( α + β ) / (1- αβ ) ] |
|
Sự khác biệt của góc Arctan α và β |
arctan α – arctan β = arctan [ ( α – β ) / (1+ αβ ) ] |
|
sin của arctan x |
sin ( arctan x ) = x/ căn (1 + x^2) |
|
cosin của arctan x |
cos ( arctan x ) = 1/ căn (1 + x^2) |
|
lập luận đối ứng |
|
|
Arctan x được suy ra từ arcsin x |
arctan x = arcsin x/ căn (x^2 + 1) |
|
Đạo hàm của arctan x |
|
|
Tích phân không xác định của arctan x |
|
Công thức tính đạo hàm của hàm số y = arctan x
Trong toán học, bên cạnh những bài toán có kết quả giới hạn, còn có vô số bài toán thuộc tập vô hạn, tức là tập chạy đến vô cùng. Điều này gợi ý ta cần tìm giới hạn của các dãy số đó. Từ đó nảy sinh các khái niệm về giới hạn lim và các công thức đạo hàm.
Đạo hàm được định nghĩa là tỷ lệ giữa số gia của hàm đó với số gia của đối số đó tại một điểm cụ thể x0, khi đó số gia của đối số gần bằng 0 là đạo hàm của hàm y = f (x) tại x0. Đạo hàm được ứng dụng rộng rãi trong việc giải các bài toán lượng giác, các bài toán thực tế trong các lĩnh vực vật lý, hóa học, sinh học hay kỹ thuật, đặc biệt là Đạo hàm Arctan X.
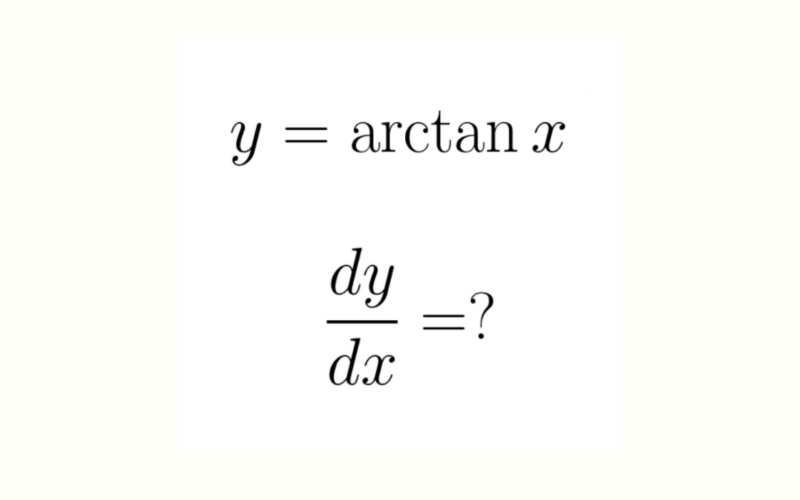
Quy tắc đạo hàm chung
Nói đến quy luật dẫn xuất tức là nói đến một hệ thống các quy tắc chung nhất mà các em cần nhớ. Khi đó bạn mới có thể hiểu và xây dựng được các công thức đạo hàm từ cơ bản đến nâng cao, chẳng hạn như Đạo hàm Arctan X.
Hệ thống quy tắc tính đạo hàm bao gồm 6 quy tắc sau:
-
Quy tắc đạo hàm để cộng và trừ nhiều hàm: (u + v – w )’ = u’ + v’ – w’
-
Quy tắc đạo hàm cho hằng: (ku)’ = ku’ trong đó k là hằng, u là hàm
-
Đạo hàm quy tắc nhân hai hàm số (uv)’ = u’.v + u.v’
-
Quy tắc đạo hàm của phân số (u/v)′=(u′v – uv’)/v^2
-
Quy tắc đạo hàm hàm nghịch đảo(1/v)′=−v′/v^2
-
Quy tắc đạo hàm của hàm hợp y(u(x): [y(u(x))]’ = [y(u)]’.[u(x)]’
Trong đó, ký hiệu dấu phẩy phía trên có nghĩa là ký hiệu phái sinh. Ký hiệu u; v ; w là các hàm u = u(x); v = v(x); w = w(x).
Cách tính đạo hàm của hàm số y = arctan x
Trong các phần trên, chúng tôi đã giới thiệu hàm cơ bản y = arctan x và các quy tắc tính đạo hàm. Vậy đạo hàm của hàm y = arctan x là gì? Nó được tính như thế nào? Hãy cùng tìm hiểu ngay trong chuyên mục này nhé!
Để tính đạo hàm của hàm y = arctan x, ta sử dụng định nghĩa của hàm arctan x.
Với tan y = x, lấy đạo hàm hai vế theo biến x ta được:
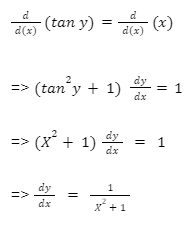
Từ đó cách tính đạo hàm của hàm số y = arctan x là:
![]()
Một số dạng bài tập tự luyện
Trên đây là cách chứng minh đẳng thức Đạo hàm Arctan X. Để hiểu sâu hơn và có thể áp dụng vào thực tế, chúng ta cùng đến với một số bài tập tự luyện cơ bản như:
-
Thực hành tính đạo hàm của hàm y = arctan x như đã định nghĩa ở trên.
-
Các bài tập liên quan đến các công thức tính đạo hàm, tìm giới hạn lim của hàm số làm quen với dạng tính đạo hàm. Từ đó áp dụng vào các bài toán về dữ liệu arctan.
-
Áp dụng trong các bài thực hành về tính quãng đường và gia tốc trong vật lý.
Đạo hàm Arctan X là một công thức đạo hàm quan trọng và khá khó nhớ. Vì vậy, để có thể nhớ lâu chúng ta cần phải thực sự hiểu và thực hành nó thường xuyên. Qua bài viết này, chúng tôi hi vọng đã cung cấp cho các bạn những kiến thức bổ ích về dẫn xuất arctan.




