Chu vi tứ giác là kiến thức khá rộng, bởi vốn dĩ hình học này có rất nhiều thể loại khác nhau nên công thức tính cũng đa dạng. Vì vậy, nhằm giúp các em hiểu đầy đủ và chính xác các thông tin về chu vi hình tứ giác, mời các em cùng manta.edu.vn tham khảo bài viết dưới đây.
Công thức tính chu vi tứ giác
Sau khi hiểu tứ giác là gì? thì một trong những bài tập thường gặp của phần hình học này là tính chu vi. Tuy nhiên, do có nhiều loại hình tứ giác khác nhau nên công thức tính chu vi rơi vào các loại sau:
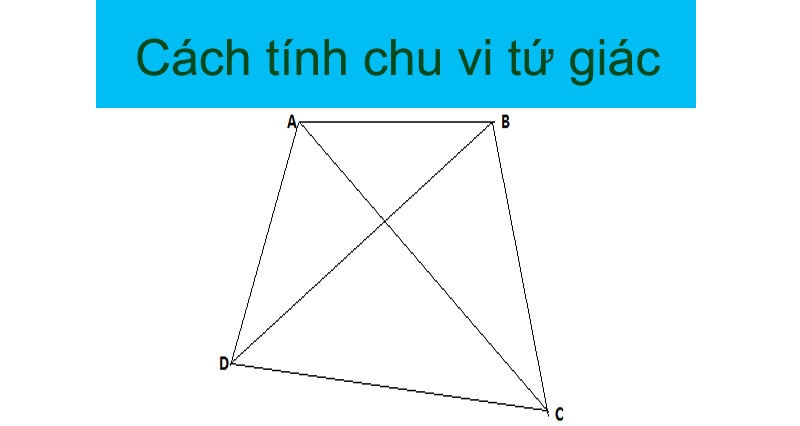
Công thức tính chu vi tứ giác đều
Với một tứ giác đều khi tính chu vi sẽ bằng tổng độ dài của 4 cạnh. Đặc biệt:
P= a + b + c + d (đơn vị)
Phía trong:
-
P: Chu vi tứ giác
-
a, b, c, d: Độ dài bốn cạnh của tứ giác.
Ví dụ: Cho tứ giác ABCD có độ dài các cạnh AB = 3cm, BC = 5cm, CD = 4cm, AD = 6cm.
Chu vi tứ giác ABCD:
P = 3 + 5 + 4 + 6 = 18(cm)
Công thức tính chu vi tứ giác đặc biệt
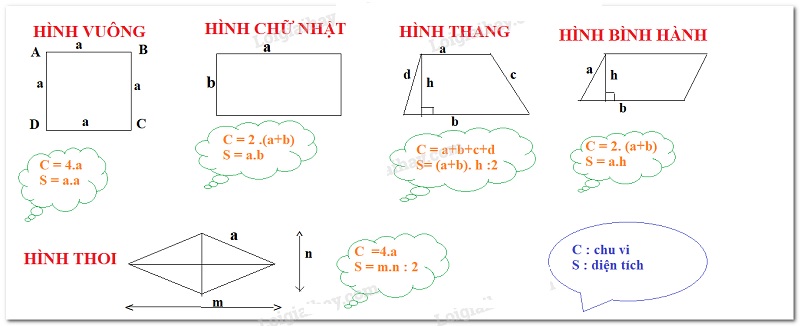
Với các tứ giác đặc biệt gồm các hình: vuông, hình thoi, hình chữ nhật, hình bình hành, hình thang. Về cách tính chu vi các hình này khá đơn giản như sau:
Chu vi hình thang có độ dài 4 cạnh a, b, c, d
P = a + b + c + d
Chu vi hình bình hành, hình chữ nhật
P = 2.(a + b)
Chu vi hình vuông, hình thoi:
P = 4.a
Phía trong:
-
P: Chu vi tứ giác đặc biệt
-
a, b, c, d: Độ dài cạnh của tứ giác
Tại sao cần tính chu vi tứ giác?
Công thức tính chu vi hình tứ giác không chỉ đơn thuần được áp dụng để giải toán trong chương trình học. Bên cạnh đó, công thức này còn được áp dụng vào thực tế để giải quyết các công việc cụ thể như xây dựng, thiết kế, v.v.
Vì vậy, để giúp các em nâng cao hiệu quả học tập cũng như hỗ trợ tốt cho tương lai của các em thì việc nắm chắc các kiến thức về chu vi hình tứ giác là vô cùng quan trọng.
Các phép tính về chu vi của một tứ giác
Đối với trẻ tiểu học, kiến thức thường chỉ ở dạng cơ bản. Như vậy đối với kiến thức tính chu vi hình tứ giác sẽ có các dạng bài tập liên quan sau:
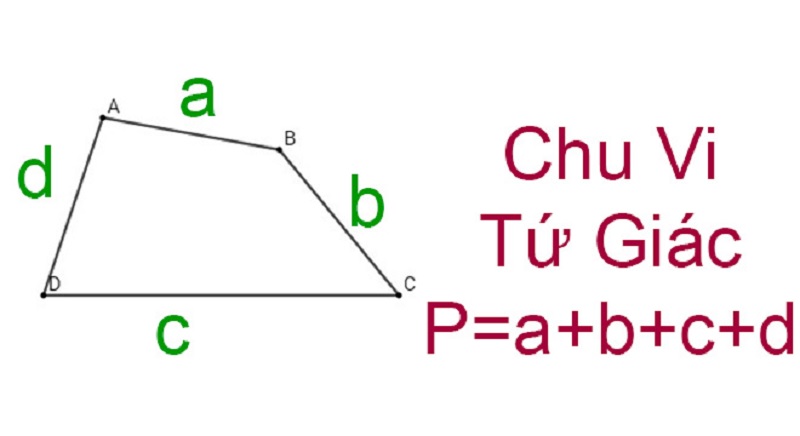
Dạng 1: Cho độ dài các cạnh để tính chu vi hình tứ giác
Đây là dạng bài tập cơ bản nhất, khi giải bài toán sẽ đưa ra thông tin về độ dài các cạnh của một hình tứ giác và yêu cầu trẻ tính chu vi hình tương ứng. Vì vậy, bạn chỉ cần áp dụng công thức tính chu vi P = a + b + c + d để tính chính xác.
Ví dụ: Tính chu vi tứ giác có các cạnh sau:
5dm, 3dm, 6dm, 4dm
3cm, 5cm, 4cm, 3,5cm
Dung dịch:
Áp dụng công thức tính chu vi ta có:
P = 5 + 3 + 6 + 4 = 18dm
P = 3 + 5 + 4 + 3,5 = 15,5cm
Dạng 2: Cho chu vi, tìm độ dài cạnh
Bài tập này sẽ ngược lại với dạng 1 ở trên, khi đề bài sẽ cho chu vi hình tứ giác và yêu cầu tính độ dài cạnh. Vậy cũng sẽ dựa vào công thức P = a + b + c + d để tính cạnh tương ứng.
Ví dụ: Cho tứ giác MNPQ có chu vi là 52 cm, tổng độ dài hai cạnh MN và NP là 21 cm. Tìm tổng độ dài hai cạnh PQ và QM
Dung dịch:
Ta có chu vi tứ giác MNPQ là: P = MN + NP + PQ + QM = 52
MN + NP = 21 P = 21 + (PQ + QM) = 45 (cm)
Tổng độ dài hai cạnh PQ và QM là: PQ + QM = 52 – 21 = 31
Đáp số: 31cm
Dạng 3: Tính chu vi tứ giác đặc biệt
Ở dạng bài tập này, các em sẽ được cho một hình tứ giác cụ thể như hình vuông, hình chữ nhật,… kèm theo các số liệu về cạnh, yêu cầu tính chu vi hình đó. Vì vậy tùy từng hình sẽ áp dụng công thức tương ứng để tính toán chính xác.
Ví dụ: Cho một mảnh đất hình vuông có cạnh tương ứng là 12cm. Tính chu vi mảnh đất đó.
Dung dịch:
Mảnh đất hình vuông có cạnh tương ứng là: P = ax 4 = 12 x 4 = 48cm.
Đáp số: 48cm
Bài tập toán liên quan đến chu vi hình tứ giác cho bé luyện tập
Dưới đây là một số bài tập về tính chu vi hình tứ giác để các em vận dụng các kiến thức trên vào thực hành:

Bí quyết giúp bé học và nhớ kiến thức chu vi hình tứ giác hiệu quả
Đối với trẻ tiểu học, thường kiến thức liên quan đến chu vi vẫn còn khá cơ bản. Nhưng do có nhiều tứ giác khác nhau nên lượng kiến thức đã học khá nhiều. Vì vậy, để giúp trẻ nâng cao hiệu quả học tập, cha mẹ có thể áp dụng một số bí quyết sau:
Đảm bảo rằng con bạn nắm vững kiến thức cơ bản về chu vi của một hình tứ giác
Để có thể giải được bài tập tứ giác và áp dụng vào thực tế một cách chính xác, đòi hỏi các em phải nắm vững những kiến thức cơ bản liên quan đến chúng. Bao gồm: Tứ giác là gì, các dạng tứ giác, công thức tính chu vi, các dạng bài tập,…
Để làm được điều này, cha mẹ nên đồng hành cùng con trong việc học, thường xuyên đặt câu hỏi liên quan xem con nhớ kiến thức đến đâu, tra sách vở,… Điều này sẽ giúp bạn biết được học lực của con. đồng thời biết được bé còn yếu kiến thức nào để có thể củng cố kịp thời.
Cùng bé luyện tập, luyện tập nhiều hơn
Trong quá trình học của con, cha mẹ nên tạo điều kiện cho con luyện tập thường xuyên từ việc làm nhiều bài tập liên quan trong sách giáo khoa, internet, luyện đề thi, học thêm kiến thức mới nâng cao, tự tổ chức. tổ chức các cuộc thi nhỏ cho bé, học toán qua trò chơi…
Càng thực hành nhiều, bé sẽ dễ dàng tiếp thu kiến thức, cũng như có hứng thú hơn khi học toán bớt nhàm chán.
Phần kết luận
Trên đây là những kiến thức giúp các em hiểu rõ hơn về chu vi hình tứ giác . Nhìn chung, phần kiến thức cơ bản này sẽ có phần dễ, phần khó, chỉ cần nắm vững, nhưng những thông tin mà manta.edu.vn chia sẻ sẽ giúp các em chinh phục bài tập một cách hiệu quả nhất. Chúc các bé có những giờ học vui vẻ.



